Rubik cube problem solving with mixed integer linear programming
Introduction:
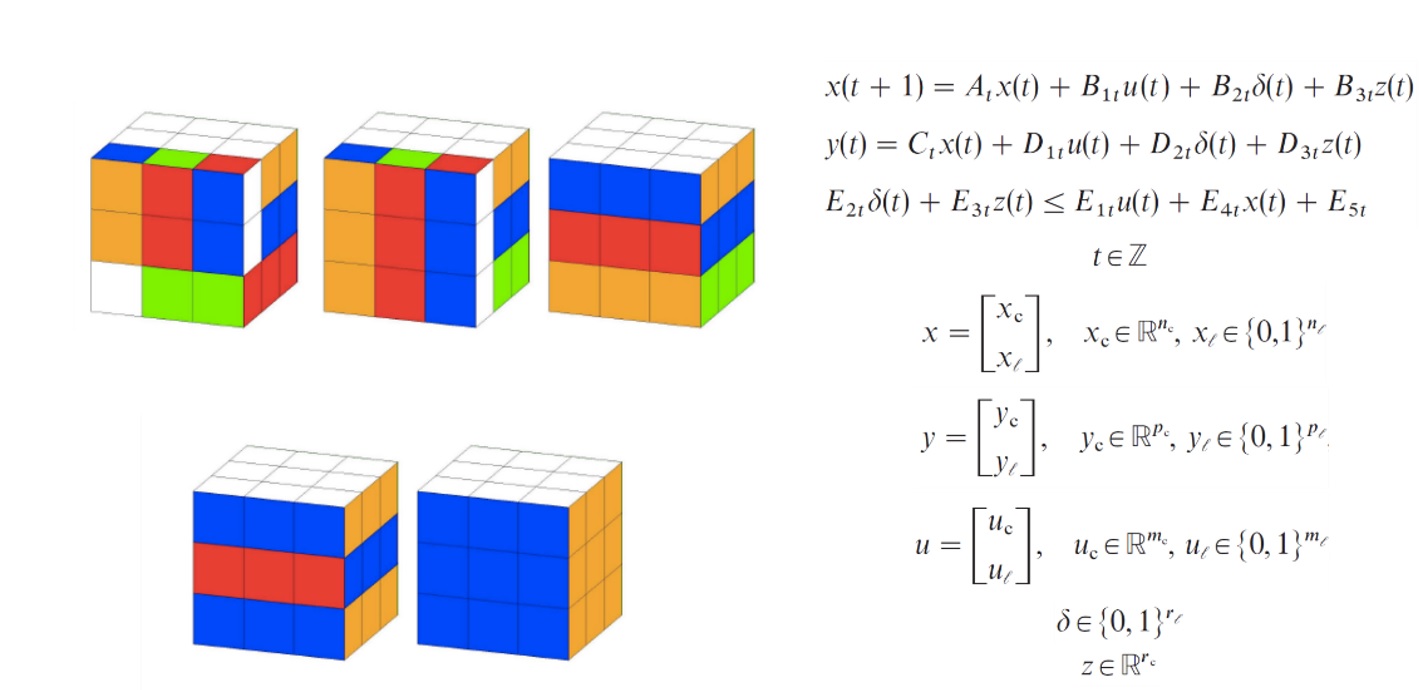
The Rubik cube is a three-dimensional combination puzzle invented by Emo Rubik in 1974. Nearly anyone in their life has tried to solve the Rubik cube but has almost always failed in their first try because of disorderly cube rotations. Every year dozens of competitions worldwide are held with the main goal being to solve the Rubik cube as fast as possible. There are lots of easy algorithms that enable players to solve any configuration but the interest in solving the problem doesn’t solely reside on the competitors’ side. There is a huge academic interest for designing efficient algorithms in as less moves as possible. In this assignment, students will develop a mathematical algorithm for solving the Rubik cube using mixed integer linear programming (MILP).
By handling the formulation of transitions of the cube part’s ordering in the form of a mathematical model of a dynamical system followed by the optimization problem associated with the model, students will learn about the possibilities of how generic mathematical optimization algorithms can be used in designing “intelligent” predictive control algorithms.
Tasks:
-
To model the Rubik cube as a discrete dynamical system with cube’s rotations as inputs and all the subsequent states of each of the cube’s parts as outputs following the specified inputs
-
To get acquainted with the desired mixed integer linear programming interface (preferably IBM CPLEX)
-
To formulate the problem as a mixed integer linear program using the above mentioned model and solve it with the chosen MILP interface
-
To design a web graphical interface with the initial configuration as the input and the list of optimal moves as the output
Additional information:
- Number of students: 1
- For undergraduate or graduate students


 Pristupačnost
Pristupačnost